Estadística desde cero: Clasificación de variables, medidas de tendencia central, tablas de frecuencias y tipos de gráficos
Una guía para el que empieza
Tiempo estimado de lectura: 5 minutos
Las variables, las medidas de tendencia central y los gráficos forman parte de la estadística descriptiva, llama así, porque su función es describir el comportamiento de una serie de datos obtenidos en una muestra poblacional.
La estadística puede ser descriptiva o inferencial. La descriptiva es un conjunto de herramientas que permite la simplificación de los datos de una muestra, cuanto mayor sea el número de datos, mayor será su utilidad. La inferencial analiza los datos para la toma de decisiones. En este espacio trabajaremos con la estadística descriptiva.
Mediante este tipo de estadística es posible identificar patrones en el comportamiento de los datos y así poder tomar decisiones acertadas en el campo que se trate.
Por medio del uso de los gráficos es posible transmitir la información de una manera sencilla y comprensible.
En este espacio verás un compilado de las diferentes herramientas con que cuenta el analizador de datos básicos.
Clasificación de variables

Las variables son características o propiedades que se pueden observar y medir en individuos o en objetos de estudio. Un individuo es la unidad estadística seleccionada por diferentes tipos de muestreo.
Existen dos grandes tipos de variables: cualitativas y cuantitativas. Las primeras indican características que no se pueden medir numéricamente, sino únicamente describir, y las segundas indican características que se identifican mediante valores numéricos.
Las cuantitativas, a su vez, se clasifican en continuas o discretas. Estas indican número enteros, y las continuas indican números con posibilidad infinita de decimales entre ellos.
La tabla muestra un conjunto de variables sobre los salarios y tipo de contratación de un grupo de colaboradores de una empresa en Estados Unidos.
En primer lugar se muestra la variable "Sexo" (hombre o mujer), que es de tipo cualitativo, dado que se representa con una denominación, y no con un número. En seguida se muestra la variable "Contrato", que también es de tipo cualitativo. Después se muestra "Salario anual", "Meses de experiencia laboral" y "Meses desde el contrato", variables de tipo cuantitativo, ya que se representan con números.
Las variables cualitativas se clasifican a su vez en nominales (sin orden, por ejemplo hombre/mujer) y ordinales (siguen un orden, por ejemplo primaria/secundaria/bachiller).
Las variables cuantitativas se clasifican en discretas (números enteros: 1, 2, 3...) y continuas (números infinitos: 1.2, 1.8, 1.85, 1.99...)
Tipos de muestreo
Los individuos se seleccionan por medio de muestreo aleatorio o no aleatorio.
Los aleatorios son: simple (al azar), sistemático (el primero al azar, los siguientes cada cierto número), estratificado (categorías), por conglomerados(elección al azar a partir de grupos con características similares).
Los no aleatorios son: de conveniencia (elegidos para pruebas piloto), de bola de nieve (se reclutan de boca en boca), por cuotas (individuos representativos), accidental (sin intención), de juicio personal.
Tablas de frecuencias

Las tablas de frecuencias son recursos para organizar los datos de una forma comprensible para el analizador.
Pueden ser simples o agrupadas. Las simples muestran los posibles datos uno por uno, siendo útiles para muestra pequeñas (menos de 30 datos) mientras que las agrupadas muestran intervalos de datos, resultando útiles para conjuntos grandes de datos (más de 30 datos). En este espacio se ejemplifican dos tables de frecuencias, una para "salario", que es de tipo cuantitativo, y se muestra de forma agrupada, y otra para "Tipo de contrato", que es de tipo cualitativo y se muestran las posibles observaciones sin agrupar (temporal, anual, indefinido).

Términos estadísticos
Dato: valor de una observación.
Intervalo de clase: división de los datos en rangos para resumir las observaciones.
Frecuencia relativa: Porcentaje que representa un dato o intervalo dentro de la muestra.
Frecuencia relativa: Porcentaje que representa todos los intervalos debajo de ese.
Medidas de Tendencia Central

Las medidas de tendencia central (MTC) son parámetros que indican la distribución estadística de una muestra de datos. Se trata de tres variables que reciben el nombre de media, mediana y moda.
La media se refiere al promedio de los valores obtenidos.
La mediana indica el valor que divide a los datos a la mitad del valor más alto al más bajo.
Y la moda indica el valor que se repite con más frecuencia.
En este ejemplo se muestra la media, mediana y moda para la variable "Salario mensual".
Se ordenan las observaciones (los datos) de menor a mayor para identificar la posición de las tres medidas de tendencia central.
Puede observarse que se encuentran colocadas en diferentes puntos de la serie de datos, lo que a simple vista deja ver que se trata de una distribución no paramétrica, aquella en la que las tres medidas son no coincidentes.
Medidas de dispersión
A partir de las medidas de tendencia central podemos conocer las de dispersión.
Rango: diferencia entre el dato mayo y el menor, en este ejemplo 60985 - 16950 = 44035
Desviación: Diferencia entre cada dato y la media, por ejemplo: 60985 - 32704.25 = 28280.75
Desviación estándar: Desviación promedio de todas las observaciones.
varianza: Cuadrado de la desviación estándar. Esta operación matemática se hace para obtener un valor de más fácil interpretación
Cálculo de media, mediana y moda
Media: suma de los datos / número de observaciones
Mediana: valor que deja el 50% de las observaciones por debajo y al otro 50% por arriba, después de haber ordenado de menor a mayor.
Moda: valor que se repite el mayor número de veces. Si son dos valores, se llama "bimodal".
Gráficos estadísticos
Los gráficos estadísticos son representaciones de los datos mediante recursos visuales que indican el comportamiento de los datos recabados. Existen diferentes tipos que se agrupan en: de barras, de líneas, circulares, histogramas, de dispersión, y caja y bigotes. La selección del tipo de gráficos depende tanto del tipo de datos recabados (tipos de variables), como de la preferencia del investigador, mercadólogo o persona que hará la presentación.
Histograma

Diagrama que se forma por barras. La altura de cada barra representa la frecuencia (número de repeticiones) de cada variable.
Se muestra un ejemplo de histograma para la variable de salario en dólares. Para generarla se realizó el cálculo de intervalos.
El histograma nos permite identificar visualmente la simetría o sesgo de los datos:
Simetría: Estadístico = 0
Sesgo negativo: Estadístico <0
Sesgo positivo: estadístico >0
Polígonos de frecuencias

Diagrama que se genera uniendo los puntos medios de cada barra de un histograma.
Puede apreciarse que la unión de puntos genera el mismo patrón que se observa mediante las barras del histograma.
Ojiva
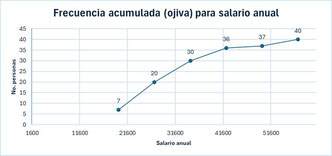
Representación que muestra las frecuencia acumulada de una variable.
Puede observarse, por ejemplo, que el 37% de los colaboradores de esta empresa ganan un salario cercano a los 51600 USD.
Gráfico de pastel

Representación circular que muestra porcentajes y proporciones con solo un vistazo.
Por ejemplo, puede observarse con solo una mirada que el 20% de los colaboradores tiene un contrato temporal.
Gráfico de frecuencia relativa

Representación de la proporción, es decir, del porcentaje, en que un valor se repite en el conjunto de datos.
Puede hacerse la misma observación que en el gráfico de pastel, pero en forma de barras.
Diagrama de tallo y hojas

Representación que organiza los datos en decenas /centenas y unidades. Es útil para datos con poca variabilidad entre decenas, pero para datos con extrema variabilidad.
En este ejemplo es notorio que el número de hojas es muy similar al número de tallos, lo que le resta ventaja a la visualización.
Gráfico de caja y bigote

Representación que identifica valores atípicos, además de comparar distribuciones y permitir evaluar la simetría de los datos en solo un vistazo.
El gráfico amarillo muestra la distribución para la variable "Contrato"; puede observarse que los datos se distribuyen de forma homogénea.
El gráfico rosa muestra la distribución para la variable "Salario"; puede observarse una mayor variabilidad para los salarios altos que para los bajos.

Si quieres profundizar sobre estadística te invito a estar atento a este blog.
Si quieres conocer más temas, por favor déjame saberlo en los comentarios.
REFERENCIAS
1. Susi profe. (2019). Tabla de frecuencias. [Archivo de video]. Disponible en: https://www.youtube.com/watch?v=xq6tBKbg3HQ
2. Saber programas (2018.) xcel - crear gráficos estadísticos en Excel según el tipo de datos [Archivo de video]. https://www.youtube.com/watch?v=cucK3A0BXEk
3. Luis Rincón. (2018). Gráfica de tallo y hojas. [Archivo de video]. Disponible en: https://www.youtube.com/watch?v=KH82_fkiOCo

Escribir comentario
Angeles Cordero (jueves, 27 febrero 2025 13:51)
Bastante bien explicado! Así paso a paso ya no me da tanto miedo la estadística, atenta a la siguiente entrada
Paulina López (jueves, 27 febrero 2025)
Buen día, cómo base para comprender la estadística me parece una información muy completa, sólo tengo una duda; ¿Los diferentes tipos de gráficos se pueden emplear de forma indistinta en cualquier caso, o algunos son más apropiados para cierto de estudios qué otros? Muchas gracias
Gómez Soberanes Patricia. (jueves, 27 febrero 2025 14:22)
Excelente explicación sobre el tema de estadística!!, me fue sencilla su lectura y entendible. Gracias.
Silvia Hernández Albirde (jueves, 27 febrero 2025 15:29)
Ahora sí lo entendí.....
Gracias
.
Cristina Hernandez Abreu (jueves, 27 febrero 2025 15:56)
La estadistica es considerada una parte de las matematicas cuya función es la de recopilar, clasificar, analizar y organizar un conjunto de datos, con el objetivo de interpretar y explicar las relaciones de fenómenos naturales y/o físicos que alteran los resultados numéricos, para buscar una posible solución. Aunque puede considerarse de facil entendimiento, muchas veces si complejidad radica en eso. Muy bien explicado, seguire atenta al blog. Saludos.
Raquel Sánchez (jueves, 27 febrero 2025 17:07)
Muy buena explicación, es algo compleja la estadística, y más cuando no sabes utilizar algunas herramientas como es Excel, que es muy útil en este caso.
Seguiré atenta al blog, saludos!
Silvia Galicia Valencia (jueves, 27 febrero 2025 17:29)
Muy interesante el tema, básico para las investigaciones en salud.
Iliana Benhumea Castillo (jueves, 27 febrero 2025 20:22)
Muy buena la explicación, sobre todo ilustrativa, la estadística se usa bastante en mi área, la nutrición, y aquí está bastante bien resumida para entender cómo aplicarla.